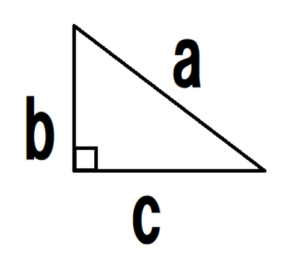
三平方の定理とは、直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを cとしたときに、公式 a 2 b 2 = c 2 が成り立つという定理です。ここで、斜辺とは、直角三角形の直角に対する対辺のことEuler 乘积公式 是一个例子 (它在 Riemann 猜想漫谈 中被用到), 本文所要介绍的 Lagrange 四平方定理也是如此, 我将在有关 Hilbert 第十问题 的文章中用到这一定理。 Lagrange 四平方定理 : 任何一个正整数都可以表示成不超过四个整数的平方之和。になるはず。 あとはABをxとおいて、三平方の定理で計算すればいいね。 4²3²=x² こいつを計算すると、 x = 5

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su
3平方の定理 公式
3平方の定理 公式- 平方完成とは 平方完成の定義と公式 まずは平方完成とはどんなものであるかを確認しましょう。 平方完成とは、 \(y=ax^2bxc\)の形の関数を\(y=a(xp)^2q\)という形に変形すること です。 早速ですが、ここで確認しておくことがあります。4 最低限覚えておくべき、基本的な数学の公式3つ 41 三角関数編:加法定理;




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
平方根 中学数学平方根の導入 中学数学平方根の導入・その2 中学数学平方根の計算ルール 中学数学平方根の値の簡略化 中学数学平方根の大小・簡略化の逆操作 平方根も因数分解もできないなら 解の公式! \ (x^28x4=0\)、\ (2x^26x3=0\) など。 それぞれの解き方を何度も練習して自分のモノにしてください! このページでは、中学3年生の数学で押さえておきたい重要ポイントである "多項式の計算" 、 "因数分解と表されるのは、 p ≡ 1 {\displaystyle p\equiv 1{\pmod {4}}} の時に限る。また、逆も成り立つ。そして、この分解は一意的である。 合成数が高々二個の平方数の和で表されるための必要十分条件は、4を法として3に合同な素因数が全て平方(冪指数が偶数)になっていることである。この定理は、フェルマーによって提起され、オイラーによって解決された。 具体的に4を法
二項式定理(英語: Binomial theorem )描述了二項式的冪的代數展開。根據該定理,可以將兩個數之和的整數次冪諸如 () 展開為類似 項之和的恆等式,其中 、 均為非負整數且 = 。(3)加法定理を使います。 (4)2倍角の公式を用いて変形します。 (5)展開し、整理する。 (6)cos 2 θに三角関数の相互関係を使います。 (7)展開、整理することで3倍角の公式になります。 〜cosの3倍角の証明〜 (1)加法定理が使いやすいように変形します。 ピタゴラスの定理 とも呼ばれてるやつね。 発見者の名前がついてるわけ。 この三平方の定理(ピタゴラスの定理)とは何かっていうと、 直角三角形の3つの辺の関係を表した公式 なんだ。 もうちょっと具体的にいうと、直角三角形には、
平方根の近似値 平方根がある範囲を小さくしていくことにより,平方根の近似値を求めることができる。 142 =196 14 2 = 196 , 152 = 225 15 2 = 225 より, 14 < √2 < 15 14 < 2 < 15 1412 = 191 141 2 = 191 , 1422 = 164 142 2 = 164 より, 141 < √2 < 142 141 < 2 < 142 このようにして計算すると, √2 2 の近似値は,小数部分が限りなく続き,より正確な値左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64 四平方の定理の証明 さっそく証明します。空間座標で考えます。三角形 a b c abc a bc の面積は点と平面の距離公式を利用して計算します。




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
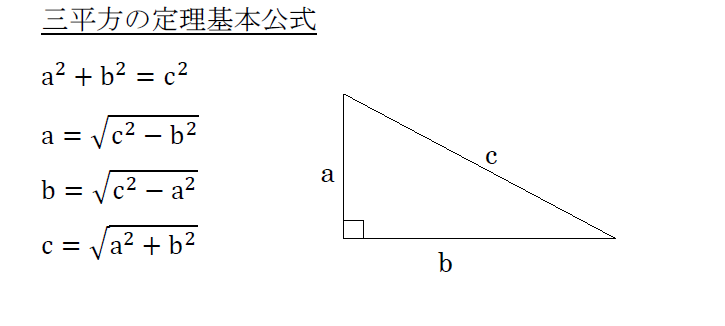
次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.)初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem)は、直角三角形の3辺の長さの関係を表す。斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は c 2 = a 2 b 2 {\displaystyle c^{2}=a^{2}b^{2}} が成り立つという等式の形で述べられる。三平方の定理(さんへいほうのていり)、勾股弦の定理(こうこげんのていり)とも呼ばれる。 ピタゴラス公式より、二点間の距離は、 d = ( 1 − 3) 2 ( 0 − 4) 2 ( − 2 − 5) 2 = 4 16 49 = 69 になります。 公式の証明: 三次元座標空間上の2点 A ( x 1, y 1, z 1) と B ( x 2, y 2, z 2) の距離を計算してみましょう。 各辺が座標軸に平行な直方体で、 A, B が頂点(のうちの2



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会




三平方の定理 覚えておきたい基本公式を解説 数スタ
3 外角定理: 外角 = 內對角 和 4 畢氏定理:直角 兩股平方和 = 斜邊的平方 逆性質:若 兩股平方和 = 斜邊的 平方, 則為直角 若直角 兩股及斜邊長度分別為 a,b,c 則 c 2 = a 2 b 2 => a 2 = c 2 b 2 => 5 直角 斜邊上的高 = 兩股積 / 斜邊 中线定理(Apollonius's theorem),又称阿波罗尼奥斯定理,是欧氏几何的定理,表述三角形三边和中线长度关系。 定理内容 三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍。 定理公式この定理の逆も成り立つ。すなわち、三角形の1辺の平方が他の2辺の平方の和に等しければ、始めの辺に対する頂角は直角である。この逆定理の成立によって、たとえば、辺の長さが3、4、5である三角形は3 2 +4 2 =5 2 であるから、直角三角形となる。この3



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
この記事の所要時間: 約 1分42秒 四平方の定理 ~三平方の定理の拡張~ 四平方の定理 三平方の定理というと, 直角三角形において, (斜辺の2乗) = (他の2辺の2乗の和) が成り立つという有名な定理 忍者が用いた三平方の定理の知恵 その昔、忍者は 敵城の周りの堀の深さを予測するのに三平方の定理を使った といわれています。 Tooda Yuuto 水面から出ている葦(あし)の先端を持ってグッと横に引っ張っていき、葦が水没するまでの距離を測ることで 三角錐の体積の公式(底面の面積×高さ×1/3)より よって h=5 と分かります。 また円の面積の公式より よって r=√3 と分かります。 また頂点から底面に垂線を下ろすと、h、r、aを3辺に持つ直角三角形ができます。 ここで三平方の定理を使うのです。 すると




無料 中3数学 発展 応用問題 問題プリント 333 三平方の定理1




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学
例如:12的平方,可以拆分为12×12=3×4×3×4=3×3×4×4=9×16=144。 3、如果数字为十的倍数,即可拆分成十乘以后来的数字,然后将这个数字本身相乘再乘以一百即可得出数据。例如:的平方,可以拆分为×=2×2×100=400。 平方常用公式 扩展资料: 平方简介:三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b とし、斜辺の長さを c とすると、次の関係が成り立つ。 c 2 = a 2 b 2 {\displaystyle c^{2}=a^{2}b^{2}}本頁面最後修訂於21年7月16日 (星期五) 0253。 本站的全部文字在創用CC 姓名標示相同方式分享 30協議 之條款下提供,附加條款亦可能應用。 (請參閱使用條款) Wikipedia®和維基百科標誌是維基媒體基金會的註冊商標;維基™是維基媒體基金會的商標。 維基媒體基金會是按美國國內稅收法501(c)(3




三平方の定理 ピタゴラスの定理




三平方の定理 の問題のわからないを5分で解決 映像授業のtry It トライイット
ここで,\(k=1\) であれば 2 平方定理が示されたことになります. \(k>1\) のとき, \(k/2 Step3 三平方の定理で計算 最後は 三平方の定理で斜辺を求めるだけ! 練習問題では、 ACは2点のy座標の差、 BCはx座標の差だよね?? つまり、 AC=51=4;フェルマーの最終定理(フェルマーのさいしゅうていり、Fermat's Last Theorem)とは、 3 以上の自然数 n について、 x n y n = z n となる自然数の組 (x, y, z) は存在しない、という定理のことである 。 フェルマーの大定理とも呼ばれる。ピエール・ド・フェルマーが驚くべき証明を得たと書き残した




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
が成り立ちます.これを「三平方の定理」といいます. 見かけ上「 斜めに見えている辺 」が斜辺なのではない 「 直角の向かい側 」にある辺=「 一番長い辺 」が斜辺四平方和定理 (英语:Lagrange's foursquare theorem) 说明每个正整数均可表示为4个整数的平方和。 它是费马多边形数定理和华林问题的特例。 注意有些整数不可表示为3个整数的平方和,例如7。実はこの定理,一般の m m m 角数に拡張できます。全ての m ≥ 3 m\geq 3 m ≥ 3 に対して「任意の正の整数は m m m 個以下の m m m 角数の和で表すことができる」のです! m = 4 m=4 m = 4 の場合がラグランジュの四平方定理(有名)です。→整数論の美しい定理7つの五




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
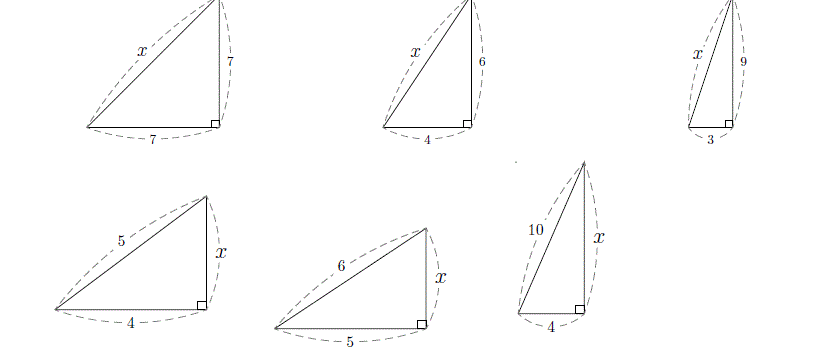
平方根(1) 問題一括 (8,085Kb) 解答一括 (9,324Kb) 平方根(2) 平方根の大小 有理数と無理数 平方根の乗法 平方根の除法 平方根の性質(1) 平方根の性質(2) 平方根の近似値 根号を含む計算 有理化 平方根の加法・減法(1) 平方根の加法・減法(2) 平方根の加法・減法中学3年数学の解説 数・素数 中学数学素数 中学数学素因数分解;三平方の定理の式( $a^2b^2=c^2$ )を見ると分かるように、三平方の定理の式は3つの辺の長さ( $a$ 、$b$ 、$c$ )でできています。 なので、直角三角形のいずれか2つの辺の長さが分かっていて、 残りの1つの辺の長さを求めたい!



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
高校数学で有名な公式の1つとして、 三平方の定理 があります。 ※三平方の定理について詳しく知りたい人は、 三平方の定理 について解説した記事をご覧ください。 この定理によれば$19$($=3 \cdot 673$)や、$$($=3^3 \cdot 5 \cdot 7 \cdot 11$)などが2個の平方数の和で表せないことが分かります。 ただし、この定理は具体的にどのような平方数の組で表せるかまでは教えてくれません。中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード・印刷 根号を含む複雑な式は、なるべく簡単な形に変形してから値を代入し、分配法則や乗法公式を使って√を含む式を計算する練習問題プリントです。




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



1




Junior High数学的 中学数学 三平方の定理を使う問題 平面図形 筆記 Clear




三平方の定理の応用




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 Rikeinvest




三平方の定理 無料で使える中学学習プリント




高校数学 三平方の定理による三角関数の計算 1 映像授業のtry It トライイット




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



1




三平方の定理の証明と使い方




三平方の定理と相似の問題 無料で使える中学学習プリント




図形問題 簡単 三平方の定理を使わずに出来る 楽しく算数 10 Geometry Youtube




中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



かみのドリル 三平方の定理




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会




三平方の定理の証明と使い方




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




中3数学 三平方の定理の応用 75度に要注意 Youtube




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




中学3年数学練習問題 三平方の定理の超基本




ピタゴラスの定理 Wikipedia




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
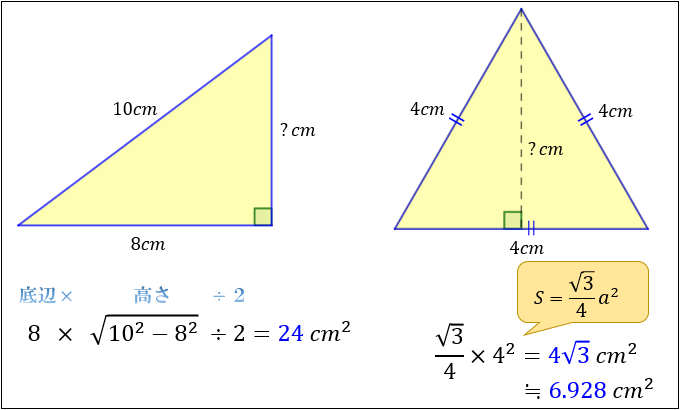



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理で辺を求める Youtube




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




國三 Junior High数学的 数学 三平方の定理 筆記 Clear




三平方の定理 自動計算サイト




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
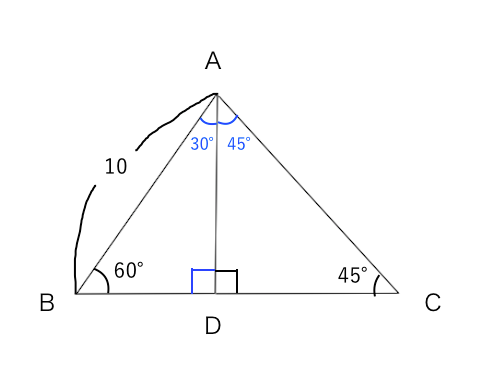



三平方の定理 練習問題 苦手な数学を簡単に
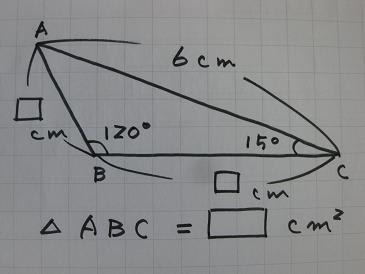



マッキーの教室 中2生徒の 三平方の定理 問題の質問に答える マッキーのつれづれ日記
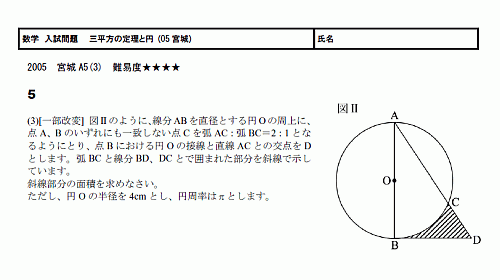



三平方の定理と円 スタディーx
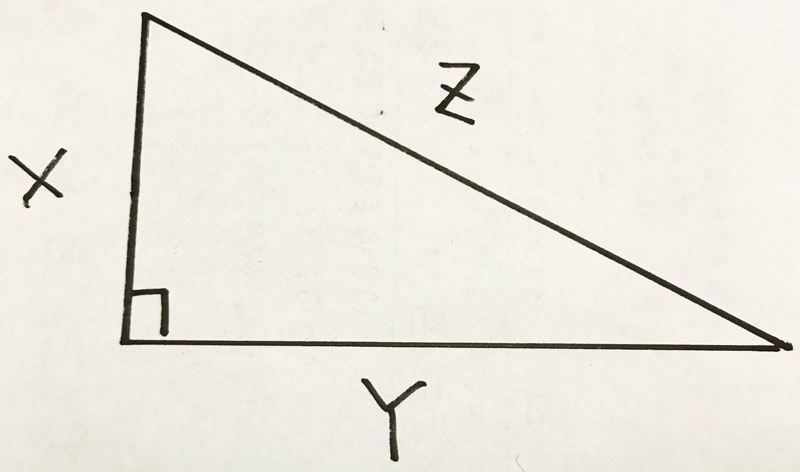



水平線までの距離 三平方の定理 21 3 19 茨木の法律相談 弁護士法人茨木太陽



3




三平方の定理です 途中式含め教えてください Clear




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



三平方の定理




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月



受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




無料 中3数学 発展 応用問題 解答プリント 336 三平方の定理4 空間図形




tan8とcos8であらわした三平方の定理の覚え方 Schoolmath S Diary




数学 中3 61 三平方の定理 基本編 Youtube




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




三平方の定理の4通りの美しい証明 高校数学の美しい物語



三平方の定理



中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
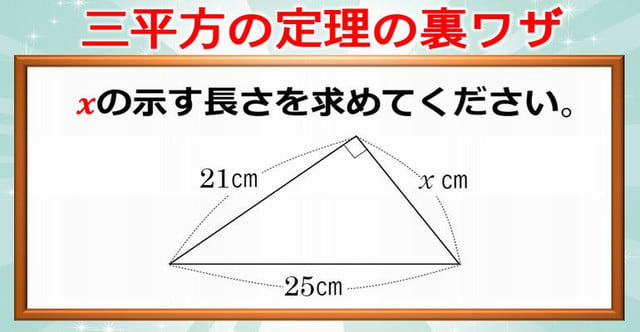



三平方の定理の裏ワザ 賢く解きたい計算の裏ワザ 暇つぶしに動画で脳トレ




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook




無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2



1




三平方の定理の証明と使い方



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




世界一わかりやすい数学問題集中3 7章 三平方の定理




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
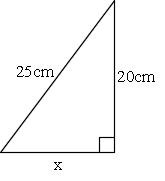



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ



Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor
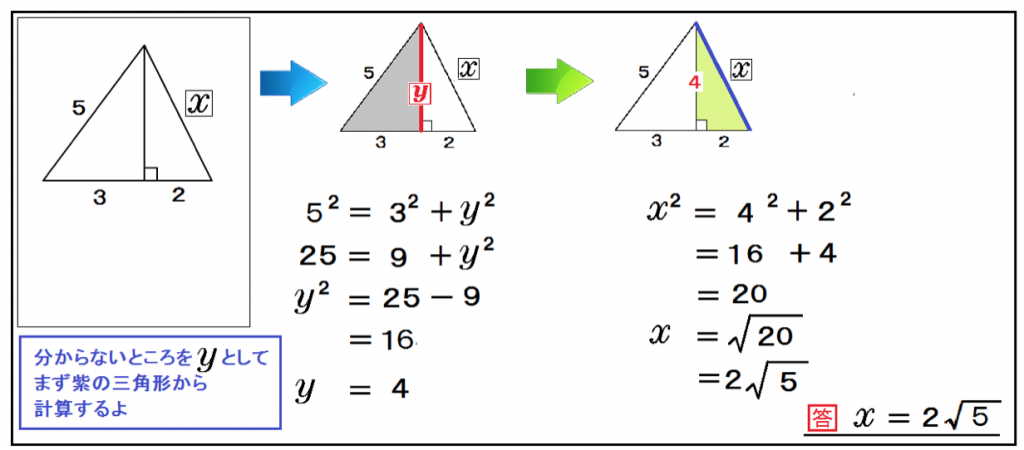



三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




三平方の定理の練習問題10問 解き方の解説 数学fun




三平方の定理 覚えること 三角定規 苦手な数学を簡単に
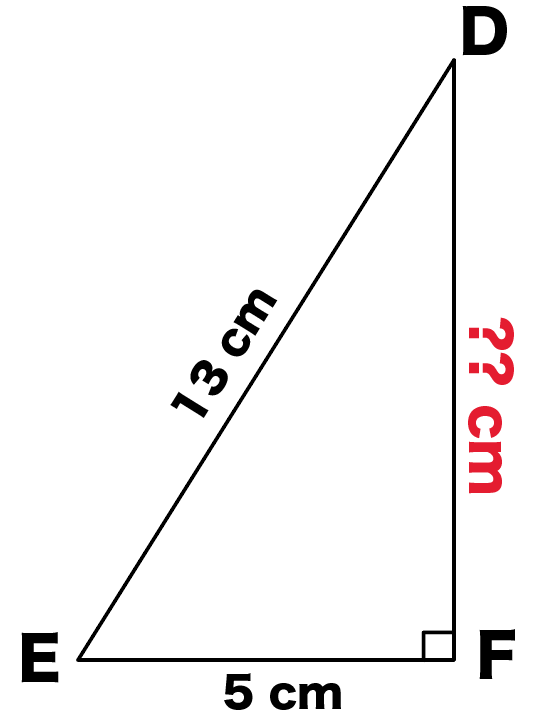



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
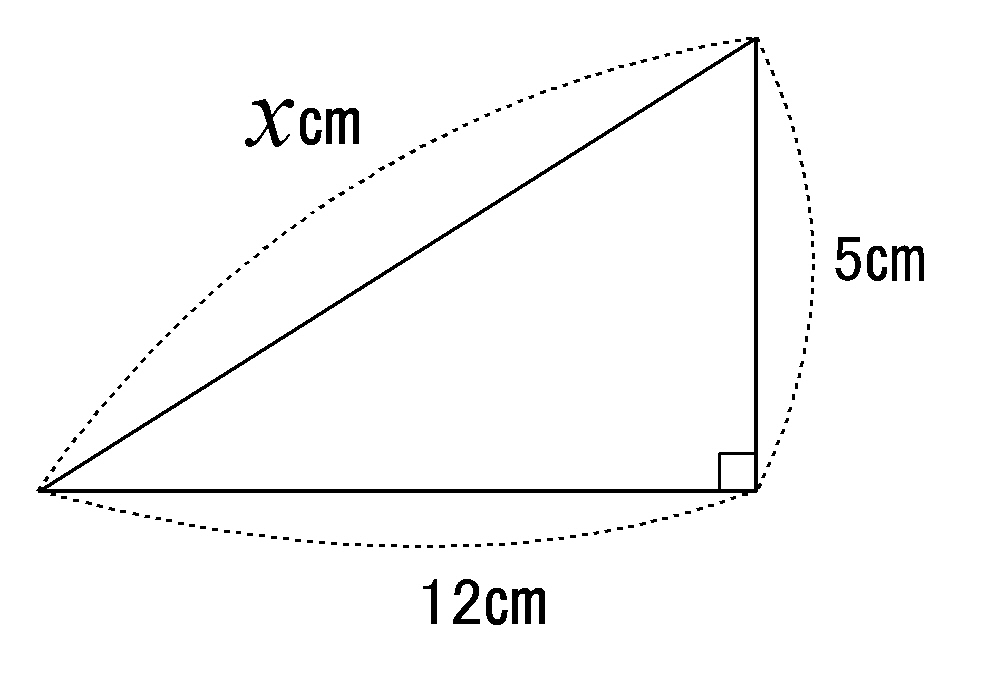



Wordで使える 三平方の定理の図 Wordで数学問題プリントを作ろう




三平方の定理を使って線分の長さを求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方



Studydoctor三平方の定理の計算 中学3年数学 Studydoctor




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学


